第三章 空域图像增强 ¶
about 2734 words 2 images reading time 14 minutes
3.1 图像增强概述 ¶
点操作:对单点像素操作,与邻域无关。模板操作的特例 .
模板操作:对图像某个区域操作。
3.2 空间变换增强 ¶
3.2.1 图像间运算 ¶
图像间算术运算:加(可平均消除噪声
图像间逻辑运算:与(mask 操作
补充知识:
色温是表示光线中包含颜色成分的一个计量单位,以温度的度量单位来记录颜色的程度,可以简单理解为颜色的温度。当黑体加热到一定的温度,黑体发出的光所含的光谱成分,就称为这一温度下的色温,计量单位为“K”(开尔文
白平衡:白色的平衡,由于人眼的适应性,在不同色温下,都能准确判断出白色,但是相机在不同色温的光源下,会出现图像偏色,与人眼看到的颜色不一致,因此需要进行白平衡处理。
白平衡算法——灰度世界算法: 以灰度世界假设为基础,认为对于一幅有着大量色彩变化的图像 , RGB 三个分量的平均值趋于同一个灰度 K。
- 确定灰度 K:取固定值 128 或 RGB 三通道的平均值。
- 计算各通道增益,即 K 与通道均值之比。
- 根据增益调整 RGB 分量。
白平衡算法——完美反射算法: 假设图像世界中最亮的白点是一个镜面,能完美反射光照。基于白点,将三通道的数值进行适当地调整,以达到白平衡效果。
- 计算每个像素的 RGB 通道之和,按大小计算出其前 10% 或其他比例的白色参考点的阈值 T。
- 计算图像三通道数值和大于 T 的点(即亮区)的各通道均值。
- 计算各通道增益,即通道最大值与亮区通道均值之比。根据增益调整 RGB 分量。
3.2.2 图像灰度映射 ¶
灰度映射函数 \(t=E_H(s)\)。
基本灰度变换:
图像求反:灰度值反转 \(t=(L-1)-s\)。
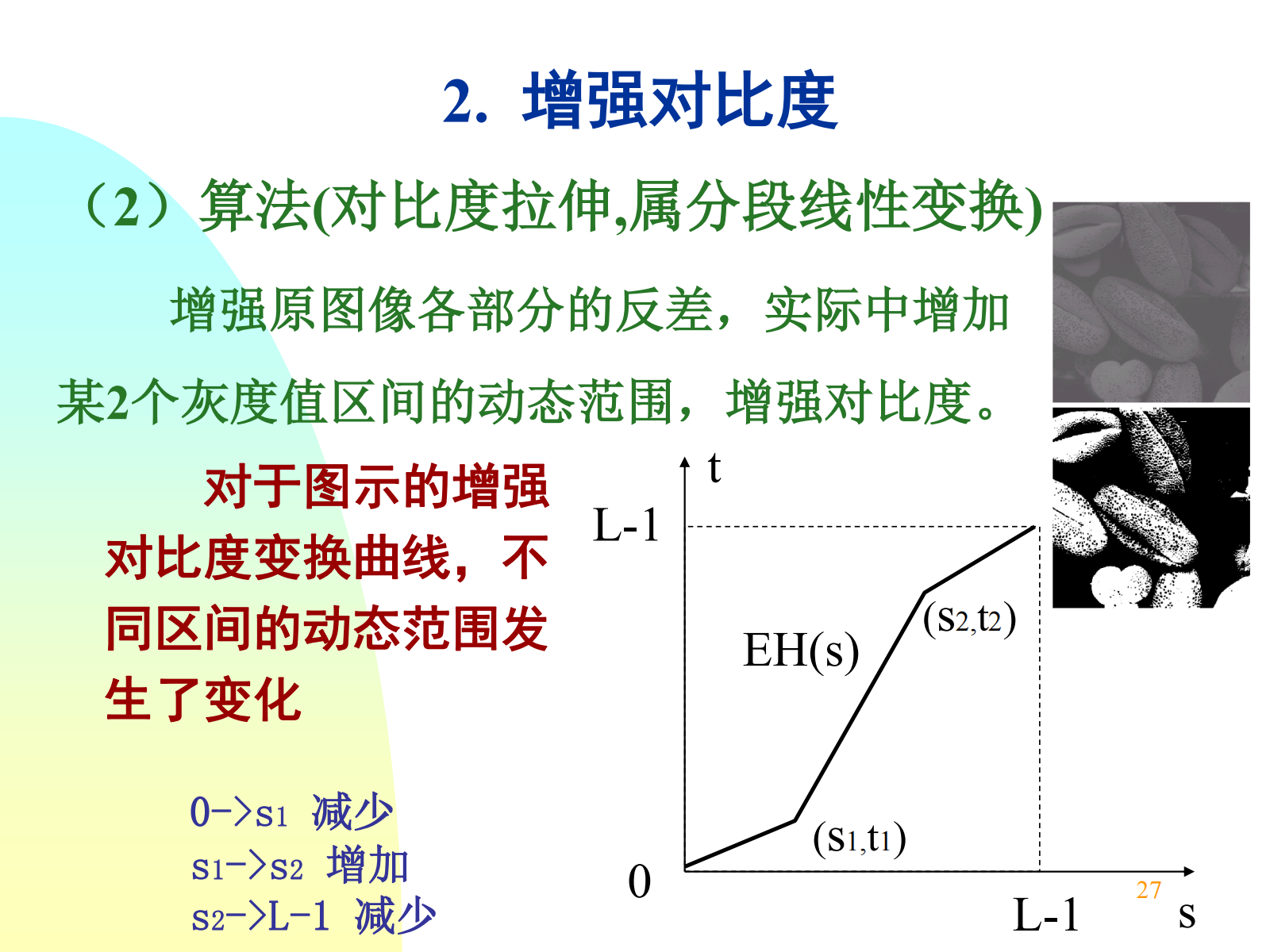
增强对比度:分段拉伸函数。
动态范围调整 ( 压缩 ):调整灰度变化的动态范围,低灰度范围的值得到扩展,高灰度范围的值得到压缩,使图像分布均匀。 常用对数变换 \(t=c\cdot\log(1+s)\)
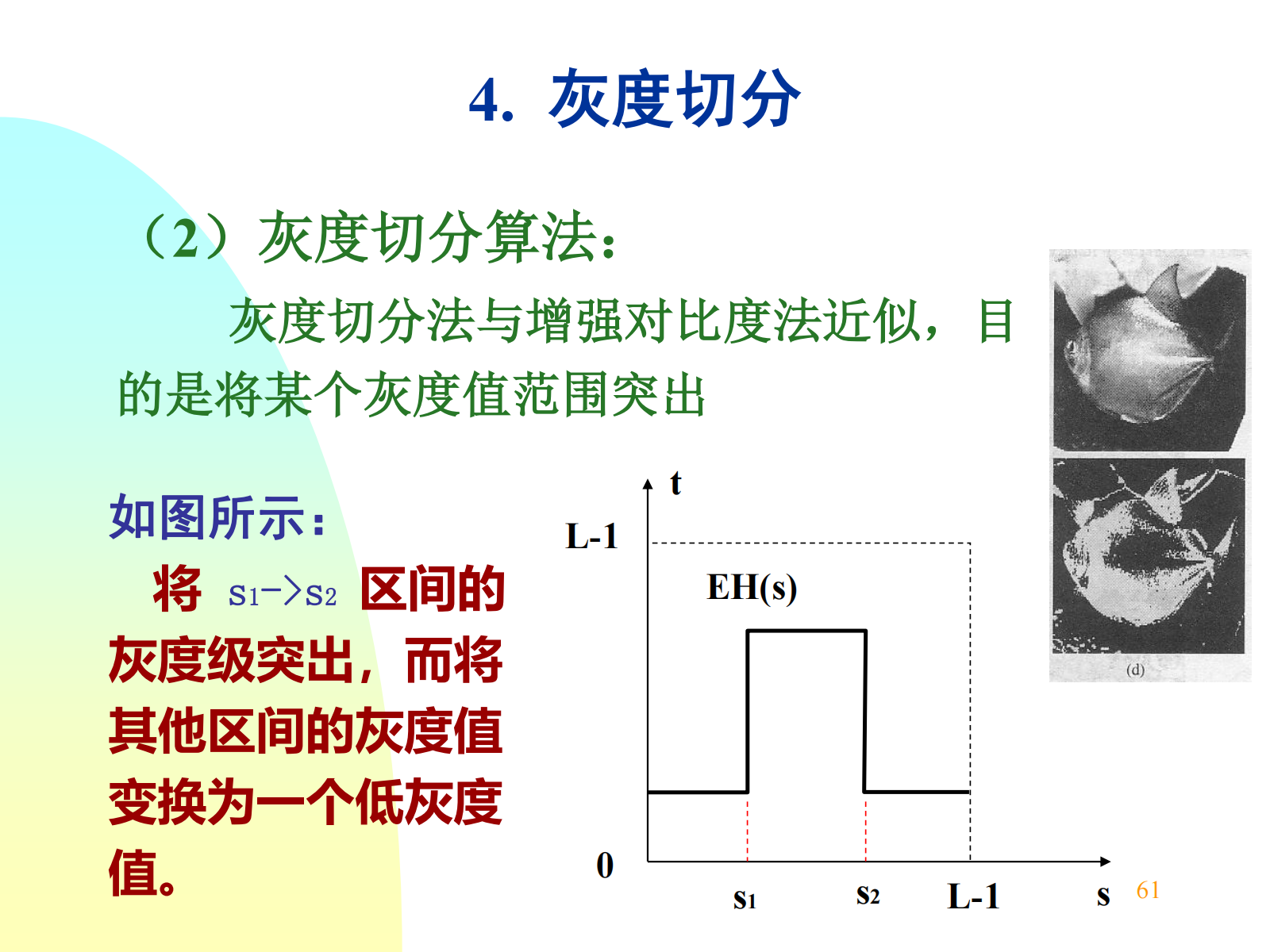
灰度切分:突出某一范围的灰度,将 s1->s2 区间的灰度级突出,而将其他区间的灰度值变换为一个低灰度值。
伽马校正:\(t=Cs^{\gamma}\),\(\gamma<1\) 提高灰度级,在正比函数上方,使图像变亮。\(\gamma>1\) 降低灰度级,在正比函数下方,使图像变暗。
3.2.3 直方图变换 ¶
图像的灰度统计直方图,\(p_s(s_k)=\dfrac{n_k}{n}\) 代表某一灰度出现的概率估计。
直方图均衡化:变换原始图像的直方图为均匀分布,使灰度层次丰富。使像素灰度值的动态范围最大,增强图像整体对比度。
变换函数应满足:在 \(0\leq s \leq L-1\) 区间内单值单增,且值域动态范围不变。( 这几乎是显然的 )
累积直方图:\(t_k=EH(s_k)=\sum\limits_{i=0}^{k}\dfrac{n_i}{n}\)。由原图像从 0 至第 k 个灰度级的概率密度函数的累积和,作为新图像的第 k 级灰度的灰度值。相当于将概率密度函数积分为分布函数。
步骤:原图像统计直方图,计算出归一化直方图,再得到累计直方图,再进行区间转换,乘上 ( 灰度级最大值 -1) 如 (256-1=255),得到原本像素和均衡化后像素的映射关系。
直方图规定化:原始直方图的灰度级概率密度函数 \(p_s(s)\),希望得到规定直方图的灰度级概率密度函数 \(p_u(u)\),步骤:
- 对原始直方图进行灰度均衡化:\(t_k={EH}_s(s_k)=\sum\limits_{i=0}^k p_s(s_i),k=0,\dots M-1\)。
- 计算能使规定直方图均衡化的变换:\(v_k={EH}_u(u_k)=\sum\limits_{i=0}^k p_u(u_i),k=0,\dots N-1,N\leq M\)。
- 求规定直方图的反变换函数 \(u={EH}_u^{-1}(v)\)。
- 原始直方图中所得到灰度级 \(t\) 代入反变换函数:\(u={EH}_u^{-1}(t)={EH}_u^{-1}[{EH}_s(s)]\)。需要找出 \(t\) 与 \(v\) 的近似值,两者近似相等时的 \(s,u\) 对应,完成从 \(s\to u\) 的变换。
3.3 空间滤波增强 ¶
3.3.1 像素间联系 ¶
欧氏距离 \(D_E(p,q)=\sqrt{(x-s)^2+(y-t)^2}\),曼哈顿距离 \(D_M(p,q)=|x-s|+|y-t|\),棋盘距离 \(D_C(p,q)=\max{(|x-s|,|y-t|)}\)。
像素的邻接:有接触,仅考虑空间关系。
4- 邻域 \(N_4(p)\):曼哈顿距离为 1,边接触,类型为 4- 邻接。
8- 邻域 \(N_8(p)\):棋盘距离为 1,边接触 + 顶点接触,类型为 8- 邻接
仅有点接触的 4 个像素点组成 D- 邻域 \(N_D(p)\),故 \(N_8(p)=N_D(p)+N_4(p)\)。
通路:由一系列依次邻接的像素组成。通路中相邻两个像素仅有邻接关系。可定义出 4- 通路,8- 通路。
像素的连接:考虑空间和属性关系,有接触且灰度值相似(相等,或者在同一个集合中取值
4- 连接:2 两个像素相似且 \(r\in N_4(p)\)。
8- 连接:2 两个像素相似且 \(r\in N_8(p)\)。
连通:由一系列依次连接的像素组成。连通中相邻两个像素有连接关系。可定义出 4- 连通,8- 连通。
连通是连接的推广,连接是连通的特例。
子集:图象中的(部分)像素的集合。
连通组元:在一个图像子集中与同一个像素相连通的所有像素构成该图像子集中的一个连通组元
连通集:如果子集 S 中只有一个连通组元,即 S 中所有象素都互相连通,则称 S 是一个连通集。一个连通集合称为图像的一个区域。
边界(轮廓
像素集合的邻接(图像子集的邻接
像素集合的连通(图像子集的连通
3.3.2 模板运算 ¶
模板卷积步骤: (1) 模板在图中滑动,中心与像素重合。(2) 模板系数与对应像素值相乘。(3) 所有乘积相加。(4) 将和赋予与模板中心对应的像素。
空域滤波增强有:线性 / 非线性,平滑 / 锐化。
常见噪声:高斯噪声,脉冲噪声(椒盐噪声
线性平滑滤波——均值滤波器:邻域平均、加权平均、高斯平均、边缘保持平滑(取中心像素的 8 个不同邻域,对每个邻域都统计其像素的灰度方差,并将灰度方差最小(方差小的邻域中像素灰度级的变化小,包含边缘的概率也小)的那个邻域中的像素均值赋给中心像素
非线性平滑滤波——中值滤波器:依靠 n*n 的模板对图像进行中值平滑处理,利用区域的中值进行平滑。让与周围像素灰度值相差较大的像素改取与周围灰度值接近的值。消除孤立噪声能力强,因为不是简单取均值,产生模糊较少,保持细节。
锐化滤波器:基于微分。
基于梯度的锐化滤波:梯度算子,X 和 Y 方向两种差分模板。实际滤波中取梯度矢量的模: \(|\nabla f|=\sqrt{G_x^2+G_y^2}\approx |G_x|+|G_y|=|z8-z5|+|z6-z5|\) 。Robert 交叉差分 \(\nabla f\approx |z9-z5|+|z8-z6|\) 。
一阶导数可以用于检测图像中的一个点是否是边缘的点。二阶导数的符号可以用于判断一个边缘像素是在边缘亮的一边还是暗的一边。一阶微分算子和二阶微分算子均可以作为图像边缘检测算子。
基于二阶微分:拉普拉斯算子,4- 邻域或 8- 邻域:
高频提升滤波:原图像叠加微分结果,等价于原图像减去积分结果 \(h_b(x,y)=A*f(x,y)-g(x,y)=(A-1)*f(x,y)+h(x,y)\) 。
最大 - 最小锐化变换
双边滤波。
引导滤波,算法步骤:( 输入图为 p,引导图为 I,输出图为 q)
- 设定一定步长和大小的滑动窗,对每个位置的滑动窗计算期望,方差,协方差:\(E[p],E[I],Var(I),Cov(p,I)\)
- 对每个位置的期望,方差,协方差计算滤波参数 \(a_k,b_k\) ,得到 ak 图,bk 图:\(a_k=\dfrac{Cov(p,I)}{Var(I)+\varepsilon},b_k=E[p]-a_kE[I]\) 。
- 再用滑动窗对引导图 I 进行滤波,得到输出图:\(q_i=\dfrac{1}{|\omega|}\sum\limits_{k:i\in \omega_k}(a_kI_i+b_k)\) 。
3.4 局部增强 ¶
局部增强:对图像某些局部区域的细节进行增强。多了一个选择局部区域的步骤。
直方图变换局部增强:先将图像分成一系列小区域(子图像
基于均值和方差的局部增强:利用像素邻域内像素灰度的均值和方差。